DTACK GROUNDED #16
January 1983

THIS YOU MAY NOT BELIEVE, but you can now buy a software package called 'The Bridge' for a VAX. This package simulates in (VAX) software the operation of an 8080 running CP/M. Now, the VAX is a fast machine but not fast enough to simulate an 8080 at full 8080 speeds, so the VAX will run a bit slower than a real 8080 CP/M machine. But there is LOTS of CP/M software, at LOTS lower prices than VAX software. An example cited is a DEC spreadsheet package which costs $10,000 and has a manual that is 20 inches (!) thick.

But if too many users (VAX terminal operators) call up that simulation, the VAX slows down such too such. So the same company which sells the software package also sells a 'Z board' which contains 4 Z80s, each with its own 64K RAM, which plugs into the VAX so that the VAX can run 8080 code more efficiently...

Isn't that wonderful? (Source: Electronics/Oct 6, 82 pp52-3.)

A LITTLE FLU BUG caused us to put the last newsletter to bed two pages prematurely. As a result, we learned 3 hours too late (moments before we headed home to treat the bug with the assistance of Dr. Calvert Fitzgerald) that HP had not been overtaken by in attack of rationality and offered a high performance computer at a reasonable price. The price we quoted, while real, does not permit turning on the computer and running a program,

You see, HP's 68000 BASIC interpreter occupies over 200K so you need the 512K version to be able to run the machine. If you have been paying attention to this newsletter you might suspect that HP wants an extraordinarily high price for those 24 additional 64K DRAMS needed to upgrade from 128K to 512K. Well, your suspicions are correct. In fact, there are a bunch of other hidden goodies you will need to pay (and pay and pay and..) for. Business as HP usual, in other words.

The Model 16 is a nice high-priced quality product which will appeal to the usual affluent HP customer. HP does make good stuff, but the price-performance just ain't there. And the Model 16 is NOT going to shoot down LISA (can we claim that the bug affected our judgement?).

ANOTHER NEWSLETTER EDITOR called us a '68000 fanatic' in his rag. We wrote back and explained that our writings were reasonable and carefully thought out and that we were really moderate in our views. We also threatened to sic our twin attack teddy bears, DTACK and Grounded, on him if he called us a fanatic again. He wrote back: "Attila the Hun was a moderate in his own way, too!"

Tsk.

Page 7, Column 1

AN OPEN LETTER TO MOTOROLA:

The 68000 that you released commercially two years ago is a very nice and very high performance part. As of Dec '82 that is also the perception of the general public. General public meaning that group of electrical engineers, computer/peripheral designers and software types involved in what we loosely refer to as 'this industry'. We believe that this perception may well be in danger soon.

What we mean is that, within the next two months, the 'general perception' of the 68000 may be that of a slow part. You and we know that this is not the case but future 'design wins' depend upon the perception of the general public.

Let us discuss how this situation has developed. You know and we know that the potential sales of the 68000 in the personal computer marketplace are a very small percentage of (potential or real) total 68000 sales. You know and we know that most 68000s will be designed into intelligent peripherals and controllers for IBM, Honeywell and such, and that they will be buried away out of sight. Most 68000 chips are sold for such 'invisible' applications.

All things being equal, it is certainly sensible to concentrate your sales effort where the bulk of the sales are. Only a dummy would do otherwise. The problem is, all things are NOT equal.

Although the personal computer marketplace accounts for a negligibly small portion of 68000 sales, either real or potential, it is a spectacularly VISIBLE marketplace. Those hidden away 68000s are essentially INVISIBLE.

The people who are the decision makers for 'design wins', such as circuit design engineers and the engineering managers and the business managers are about to be shocked by the poor performance of a certain 68000 machine which is about to be introduced by a major personal computer manufacturer.

How can a 68000-based machine have poor performance? Read the front page of this newsletter. The way to make a 68000-based machine run slowly is to sabotage the software. Who has sabotaged 68000 software? Well, the original culprit was an outfit which you may have heard of called Motorola.

You see, Motorola originally marketed the 68000 EXCLUSIVELY as a minicomputer substitute and therefore supported the development of high-priced minicomputer type software EXCLUSIVELY. As a result, when the 68000 became an affordable part to use in a cheap personal computer, as it is now, the only available software was the high priced minicomputer stuff. (It is too bad that no one at Motorola foresaw the inevitable result of advances in IC production capability. The inevitable result? Why, cheap 68000s of course!)

Page 7, Column 2

Back to that certain 68000 machine which is about to be released by a major personal computer manufacturer: That company is watched very closely by the Wall Street Journal for reasons which we need not discuss here. Shortly after it becomes evident that it is SLOW for a 68000 based machine there will be a story by the Journal on the front page of the second section. And the business managers in this industry are going to read that story.

This same information will also be published in those journals associated with our industry such as Electronics and BYTE (both McGraw-Hill periodicals) and Infoworld. This is where the working engineers will learn about it. What magazines the engineering managers read we don't know, but what we are really saying is that this is not going to be a secret.

How do we know this? There was a review of the Fortune 68000-based machine in a recent Interface Age magazine in which the 68000 machine proved slower than some 8 bit varieties. A very recent issue of Infoworld published a short interview with Fortune management in which the reasons for the slowness of the machine was questioned. The reply was, "Oh, we are fine-tuning the operating system for speed" which is much more polite than "Go away, boy, you're bothering me" which it really means.

You don't think the industry standard BASIC uses two levels of interpretation? Check that very same Infoworld report where the Fortune spokesman specifically asserted that "their" BASIC could be transported to other processors specifically including the iAPX 286. Of course it can be transported! It is written in a sort of 'p-code' for that very purpose. And that is the second level of interpretation. And that is why the 'industry standard' BASIC is so slowww...

The thing is, not that many people read Interface Age and not that many people are following the Fortune machine closely. But there are an ENORMOUS number of people following that major personal computer manufacturer and anxiously awaiting news of its 68000 machine.

So what suggestion do we have to cure the situation? We do not have one that would be acceptable to Motorola. We know; we made a suggestion that would work and had it rejected, naturally. But Motorola should recognize the high visibility of the personal computer marketplace and not repeat its mistakes when the 68020 comes out.

Best regards, honest! (signed) your FNE

Page 8, Column 1

THE REJECTED SUGGESTION:

We suggested that Motorola invest about $300K in a 68000 BASIC with zero run-time interpretive overhead but fully interactive with the user. We then suggested that Motorola place this BASIC completely in the public domain, INCLUDING THE SOURCE CODE! Yes, we know this sort of thing just isn't done. Let as explain to you why it SHOULD be done:

It should be done because Motorola would not only be able to directly recover its dollar investment but would also gain ENORMOUS profits in an indirect way. Let us explain how this would come about.

First, if the BASIC had high performance (it would HAVE to be a high performance package with no interpretive overhead) and if it were FREE, then every one of those 100 manufacturers of 68000 based small computers would make that BASIC available on their computers. Which would make the new BASIC the NEW 'industry standard', at least for the 68000 section of the industry.

There would be a large demand for a BOOK describing the BASIC, including explanations of how the routines work and including the complete source code as a large appendix in the book. Such a book would recover at least $10 per copy for the publisher (Motorola), so that only 30,000 copies need be sold to recover the up-front investment.

IF the BASIC is GIVEN AWAY and so becomes ubiquitous, the demand for the book would be much greater than a mere 30,000 copies. It would not be unreasonable to expect to eventually recoup 10 times the original investment DIRECTLY..

But the INDIRECT profits would be enormously greater. First, each of the small 68000 based machines such as the SAGE and Fortune would instantly become the FASTEST personal computer available! The 'general perception' of the 68000 would be the correct one: it is by far the fastest microprocessor available for a small personal computer. The word in the general marketplace would be: You want to run fast, you use a 68000. THE RESULTING 'DESIGN WINS' WOULD BE THE MOST PROFITABLE RESULT OF IMPLEMENTING THIS SUGGESTION.

In fact, the only persons who could lose would be Motorola's competitors.

Let us consider some of the possible arguments against this program:

1. Placing the source code in the public domain would just help Motorola's competitors

   Page 8, Column 2

   Baloney! Motorola's only major competitor is Intel, and Intel's chips cannot address a large memory space directly and they do not have enough address pointers to implement the language. Such a BASIC will inevitably use threaded code during run time and use lots of pointers and 32 bit arithmetic during the interactive phase. It MIGHT be possible to 'port' the language to the National 16032 but so what? Does anyone seriously think the 68000 is threatened by the 16032?

2. There is no assurance that the BASIC mould become popular. The profits, both direct and indirect, depend on in assumed popularity.

   If the BASIC is both FAST and FREE, there is absolutely NO WAY it could fail to be popular. The only way to block it would be for some brain-damaged traditionalist at Motorola to decide at the last minute that since the language has such high performance, it should be licensed. THAT would, indeed, not merely damage its popularity but kill it dead.

3. It is not possible to write a language with the attributes described/asserted.

   It is TOO possible! We are (slowly) doing it ourselves and we have progressed far enough that we KNOW it can be done! But our resources are smaller than Motorola's (candidate for understatement of the year) and we cannot bring this off quickly enough to gain the maximum benefit for Motorola. Also, we would NOT place our work in the public domain. Instead, we would (will) publish it with copyright notices and distribute copyable disks containing the source code.

4. Maybe Motorola doesn't know HOW to write such a language? It does sound slightly unconventional.

   We have already offered to donate, it no charge, the work we have done toward implementing that language to Motorola. We here repeat, in writing, that offer.

5. This sort of thing just ISN'T DONE in this industry.

   Times change. It SHOULD be done. It should be done because Motorola would reap ENORMOUS benefits.

6. What is in this for Digital Acoustics?

   We will sell a lot more boards to work with the Apple and the Pet if such a language were available and was an industry standard (68000 section). That would produce standard APPLICATION software for 68000 machines, something which is somewhat lacking right now. Anything which makes the 68000 look more desirable will enhance our sales. We don't mind at all that it would ALSO enhance the sales of SAGE, Fortune and the other 90 manufacturers of small 68000-based computers.

Page 9, Column 1

(It is clear in retrospect that that suggestion was phrased improperly. It must have cost Motorola at least $100 million so far to develop the 68000 product line. Prudent businesspersons would invest about 15% of that sum in promotion. Promotion is whit you do to convince the public that the 68000 runs faster than a ring-tailed wowser.)

(We believe it would have been prudent to invest 2% of that promotional budget, or $300,000, in demonstration software. Since the persons making the design decisions are mostly engineers, the demonstration software should be slanted toward engineers' needs. Engineers need to solve problems and BASIC is the language of choice for engineering problem-solving. The $300,000 is for purely promotional purposes and the question of a possible direct payback is a red herring which should never have been raised.)

WANG LABORATORIES now sells over $1 BILLION in computers per year and is a FORTUNE 500 company. Wang is the ONLY computer company, as far as we know, which grew to that size from an origin of selling one CPU to set in front of one user. We think our recent experience with them might be enlightening.

We are seriously considering purchasing a replacement for our 10 year old 2200C, which is getting old and rheumy-eyed. Last issue, we told you a little about its current equivalent, the 2200 SVP. Since last issue we went to see a demonstrator SVP. The demonstration room is about 600 to 800 square feet, nicely carpeted and paneled. We forget whether there were two or just one additional model besides the SVP since that was the model we were interested in.

The SVP is HUGE! Aside from a terminal about the same size as our CBM 8032, the rest of the computer is in an absolutely HUGE cabinet with 8 inch double density double sided disks, one on each side. When we opened it up, we found that most of that size was to assure adequate cooling. After all, a computer which runs cool is a RELIABLE computer. But that huge cabinet has to be at desk height and also nearby since that's where the floppies are. And that huge cabinet will dominate any office it is in. Maybe that's the idea?

Once we got over our shock at the size of the beast, we looked around for a programming manual (a principal reason for the visit was to check for software compatibility with our old machine, especially some microprogrammed I/O instructions called $GIO). There was no programming manual in the demo room. In fact, as we looked around we realized that there was NOT ONE SINGLE SCRAP OF ANY KIND OF PAPER IN THE ROOM! Not even a snuffed out cigarette (there were no ashtrays).

Page 9, Column 2

So we went to the salesperson's cubicle, the service department AND the literature room looking for a programing manual for the SVP. There proved to be NOT ONE SVP PROGRAMING MANUAL in the building! So, we ordered one from Wang for $25. They had to send to Tewksbury Mass. for it. We got it last week (actually the salesperson delivered it personally and at no charge) and sure enough, the SVP does support those $GIO instructions. Fortunately, we did not immediately place in order because an article in this Monday's EN states that Wang is dropping its 2200 series prices to counter corresponding reductions in IBM's System 34 line. The price cuts appear to be in the 25 - 30% range but they have not yet been officially announced, so we'll wait.

Sure wish the SVP had a screen editor like our CBM 8032 and HIRES graphics like our (several) Apple IIs.

We have an associate in the local area who is well connected in the Pet world. We had an argument recently over whether Commodore's production costs for the $595 Model 64 are more or less than the production costs for the VIC 20, which is selling for as low as $168 locally. Our opinion is that the Model 64 costs MUST be higher, those eight 64K DRAMs aren't all that cheap. It is true that the 64 LOOKS easier to build than the VIC 20. Open the two side by side and you'll see what we mean.

Anyhow, this associate insists the 64 costs $20 less to build than the VIC 20, 64K DRAMs and all. Which means Commodore could market that little baby at the $150 level (discounted). That means possible BIG TROUBLE ahead for the revised Apple II if it stays pricey...

THE FOLLOWING TRADEMARKS ARE ACKNOWLEDGED: Apple, II and soft: Apple Computer Co. Pet: Commodore Business Machines. VAX and PDP11: Digital Equipment Corp. CP/M: Digital Research of CA. DTACK GROUNDED and HALGOL: Digital Acoustics, Inc.

SUBSCRIPTIONS: You can subscribe by sending $15/6 issues U.S. and CANADA or $25/6 issues elsewhere. Tell us which issue number to begin with. Make the check out to DTACK GROUNDED. The address is:

DTACK GROUNDED
1415 E. McFadden, Ste. F
SANTA ANA CA 92705

THERE IS SOME IDIOT WHO, under various pseudonyms, is constantly being quoted in various publications that the availability of computers will cause students to become mathematical illiterates. If we ever catch that guy we are personally going to bash his head in with a five pound sledgehammer!

Don't miss page 15!

Page 10, Column 1

TRANSCENDENTAL FUNCTIONS:

In this issue we are publishing in REDLANDS (???) the standard BASIC transcendentals to go with the double precision floating point package found in the last issue. This includes LOG, EXP, SQR, SIN, COS, TAN and ARCTAN.

OBJECTIVES: All of us would like to have a computational machine with infinite precision which executes in zero time and which requires no storage space. You will find such a machine sitting right next to your free lunch.

As a practical matter, we must compromise. Who decides what the compromises are? In this case, your FNE has the exclusive authority and responsibility. This takes the job both easier and harder. One is not restricted to a predetermined format, as was the case when the Microsoft compatible 9 digit package was being written. On the other hand, one likes to do a respectable job so that those DTACK subscribers and board owners who are much better mathematicians than we are will not be disgusted or excessively amused.

Accordingly, we have spent CONSIDERABLE time (to the detriment of our hardware effort) checking the accuracy of the package. This will be reported as a separate section later.

HERE ARE OUR GROUND RULES: with a 48 bit mantissa we have just over 14 decimal digits of precision. It is possible in principle to approach that precision in calculating the transcendental functions, but it is very difficult. A more realistic goal is to try for 13.5 decimal digit accuracy in general, and hope that at least 13 digits is the poorest precision obtained.

And please: let us not fight over the difference between 'accuracy' and 'precision'. We will lean heavily on the book COMPUTER APPROXIMATIONS, and in that book 'precision' is used where some of us would prefer 'accuracy'.

We must recognize that poorly conditioned numbers will reduce the obtainable precision. For instance, the sine of 0.1 can be calculated more accurately than the sine of (2PI + 0.1) since we will lose some bits of precision in the argument during range reduction.

Aha! New jargon! You will recall that transcendentals are monadic functions. (If you do NOT recall this, review page 9 of our newsletter #1.) To calculate the square root (for instance) we pass a number to the SQR subroutine by leaving it in the floating point accumulator, FPACC1. This number is called the 'argument' of the function.

Page 10, Column 2

RANGE REDUCTION: If the argument passed to the SIN subroutine has an absolute value greater than 360 degrees, we must reduce its range to less than 360 degrees. In fact, we will reduce the range down to 0 to 90 degrees before performing any significant amount of computations. This is what is meant by 'range reduction'. The range reduction process for our chosen ARCTAN algorithm is quite complex.

Except for the SQR function (which uses Newton's method) the algorithms and stored constants used in this transcendental package are mostly taken from the book COMPUTER APPROXIMATIONS by Hart et al, Wiley 1968. This book is one of the SIAM series in applied mathematics.

SHORTHAND NOTATION: The techniques used (except for SQR) involve range reduction and then calculating a Chebyshev approximation using some form of series calculation. COMPUTER APPROXIMATIONS uses a shorthand notation which might confuse the reader on first confrontation (we believe 'confrontation' is the correct term). For instance:

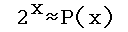
 Range   Precision     N    Index
 [0,1]     4.12        3     1040 

means that the exponent function base 2 can be calculated, over the range 0 to 1, to a precision of 4.12 decimal digits using the series form P(x) with N = 3. That series is calculated as follows:

 Fn = P0 + X * (P1 + X * (P2 + X * P3)) 

Note the nested form of the computation. This reduces error buildup due to rounding errors which might be caused using an otherwise equivalent form, say E(X) with N = 3 which would be calculated is follows:

 Fn = E0 + X * E1 + X * X * E2 + X * X * X * E3

 where E0 = P0
       E1 = P1
       E2 = P2/P1
       E3 = P3/(P1*P2) 

Finally, 'Index' refers to a particular table in the back of the book, table number 1040. This table contains the four constants, P0 thru P3. The number of constants in a given table is always one greater than N.

And if the argument is not in the range 0 to 1 then some form of range reduction must be performed to accomplish that, and the needed corrections made after the series approximation is calculated.

Page 11, Column 1

OTHER SERIES FORMS: To repeat, the nested form is used to reduce error buildup. There are other forms of series approximations used, especially X*P(Z) where Z is a function of X (often equal to X squared). The SIN function is calculated using this form, for instance. If N is equal to 3, the calculation is performed as follows:

 Fn = X * (P0 + Z * (P1 + Z * (P2 + Z * P3))) 

There are many other forms of series approximations, most of which are NOT used in this transcendental package. Perhaps we should mention the form used to calculate the logarithm function, which is P(Z * Z) or P(Z squared) where:

 Z = (X - 1)/(X + 1) 

ABSOLUTE AND RELATIVE ERROR: If T = the true value of the given transcendental function of the argument and Fn is the calculated approximation to the argument, then:

 Absolute error = T - Fn

 Relative error = (T - Fn)/T 

The following crude drawings illustrate a Chebyshev approximation of the sine function (range reduced to 0 to 90 degrees). The error is somewhat exaggerated (we hope).

ABSOLUTE ERROR

RELATIVE ERROR

Page 11, Column 2

The relative error is NOT always the appropriate error criterion. Following are the appropriate criteria for each of the transcendental functions in this package:

 RELATIVE: SQR, EXP, SIN, COS, TAN.
 ABSOLUTE: LOG, ARCTAN. 

Note that even though the LOG function passes through zero, as does the SIN function, absolute error is the appropriate error criterion.

We will now describe the calculation of the EXP and ARCTAN functions in some detail. These descriptions will be followed by 'short form' descriptions of the remaining functions and then a description of the error testing we have performed on this package and the results of that testing. Oh, yes: then we will print the source code for the transcendental package.

CALCULATION OF EXP(X):

To calculate the exponent function to the base of natural logarithms, e, we simply multiply the argument by one over the natural logarithm of two and THEN calculate the exponent of the result to the base 2.

Similarly, we can provide an exponent function to the base 10 by simply multiplying the argument by one over the logarithm to the base 10 of two and then calculating the exponent of the result to the base 2.

This means that we can easily and conveniently provide HALGOL with routines for calculating the exponent to any of the three bases 2, e and 10. And so we do!

APPLICABILITY:

For any given X along with a specified base a unique result exists. This result cannot be less than one for positive X. However, the result may be too large to be representable in the floating point format in use. In that case, an overflow message must be reported.

 IDENTITIES (from HART et al):

 eqn 6.2.19: EXP(X+Y) = EXP(X)EXP(Y)

 eqn 6.2.24: EXPe(X) = EXP2(X/ln2) or,
             EXP10(X) = EXP2(X/log2)
             where  EXPE(X) = exponent, base e
                    EXP2(X) = exponent, base 2
                    EXP10(X) = exponent, base 10
                    ln2 = natural logarithm of 2
                    log2 = logarithm of 2 to the base 10
 
 eqn 6.2.25  EXP(-X) = 1/EXP(X) 

Page 12, Column 1

DISCUSSION:

It is in general impractical for binary machines to calculate the exponent function (efficiently) in any other base than 2. To calculate the exponent of e, we use (6.2.24) and divide X by ln2 (actually we multiply by 1/ln2) and then proceed to calculate EXP2(X') where X' = X/ln2. Note that ln2 (or 1/ln2) is simply a stored constant whose value is published with great precision in HART.

We now assume that the problem is to calculate EXP2(X), referred to henceforth is simply EXP(X).

First we store the sign and set the sign of the argument positive (line 531). We also test for a zero argument (line 535). If X = 0, the result is one.

Next we reduce the range over which the value must be calculated so that a Chebyshev approximation can be applied. First we test whether the argument is ALREADY less than 1/16 (line 537). If so, no range reduction is necessary.

Next we test whether the exponent is greater than $100D. If so the argument is too large IF the sign was positive. So, if the sip is positive, we report an overflow message. In BASIC this is a fatal error and program execution stops. If the sign was negative, the result is zero and there is no error (line 511). (One over a number too large to represent is zero.)

We have chosen to reduce the range to 1/16 > R >= 0. We use R to indicate the Residue of the range reduction process. This range reduction can be accomplished by setting X equal to the sum of three parameters

 X = INT(X) + C + R 

So that, by 6.2.19:

 EXP(X) = EXP(INT(X)) * EXP(C) * EXP(R) 

Here, INT(X) has its usual meaning and C is equal one of sixteen values: zero, 1/16, ..., 15/16. R is the Residue, defined above.

Unfortunately, Hart does not contain an appropriate series approximation, so we have had to devise our own (see CONCLUDING DISCUSSION). We use N = 6 and the series form P(X). Let us suppose that EXP(R) has been calculated and continue.

The exponent of the integer of X is calculated very simply by adding the integer to the exponent portion of the floating point representation of EXP(R). The result is equivalent to multiplying EXP(INT(X)) * EXP(R). We must next determine which EXP(C) (if any) to multiply times this last result.

Page 12, Column 2

If C = 0, EXP(C) = 1 and there is little to gain by multiplying by one (line xxx). Only if C <> 0 do we multiply by one of 15 stored constants. Having multiplied by EXP(C) if necessary the result is the EXP(ABS(X)). We now test whether X was originally negative (line 585), and invert the result if so (6.2.25).

The exponent function calculation is now completed.

TRICKY STUFF:

We need to store a 17 bit number which is the integer value of 16 times the argument of EXP2(X). The most significant 13 of these bits is the integer value of the argument and the least significant 4 bits determine which of the 15 stored constants will be used (or, if all 4 bits are zero, no EXP(C) correction is performed). Because the number of bits is more than 16, we use a 'long word' (32 bit) storage area called EXPADD to store this datum.

Note that its clear (.L, 32 bits) EXPADD in line 532 in case the argument is already less than 1/16 so that no range reduction is performed. In lines 539-40 we calculate the difference between the exponent and $100D. In line 546, we fetch the highest order 32 bits of the mantissa. Since we are going to store the 17 bit integer in a 32 bit space, we need to add #15 to this difference to determine the number of right shifts to be performed. We do this in line 547. The next line shifts the 32 bits in D2 right by the count in D1. This is a very rapid method of calculating the integer of 16 times the argument.

After performing the series calculation, at line 568 we recall the 17 bit stored value, shift it four bits right to obtain the integer of the argument (rather than 16 times the argument) and add the integer value to the exponent of the series calculation result.

Then in line 571 we load the lower word (note the MOVE.W and EXPADD+2) and mask the upper 4 bits. If the result is zero we can skip multiplying by EXP(C). Otherwise, in line 577 we multiply the number by 8 to determine the address of the desired stored constant after adding the starting address of the constant table, less 8. Simple, no?

CONCLUDING DISCUSSION:

Based on the series approximations of form P(X) that ARE published in Hart, we were almost certain that a series approximation of precision 15 (or so) could be found over the range 1/8 > R >= 0 with N = 6. See for instance the progression from Index 1043 to 1023 to 1003. However, we were unable to achieve a precision of better than 12.5 or so.

Page 13, Column 1

We even tried to obtain a series with N = 7 over that same range and failed. But when we used N = 6 and reduced the upper limit of the range to 1/16 we quickly found the constants for calculation to the needed precision. Unfortunately, this requires eight more stored constants (pre-calculated values of EXP(Cn)) than would otherwise have been needed.

We are almost certain that the failure to find the desired series approximation is due to our lack of expertise (translation: we don't know what the hell we're doing).

CALCULATION OF ARCTAN(X):

There is no 'good' way to calculate the ARCTAN (or ATN) function. The problem is to select the least undesirable method. The reason we say this is that this function is the most resistant to being easily approximated using a series approximation of reasonable length.

Although there are well known series functions which eventually converge on the desired value of the function, they converge very SLOWLY. Of those series approximations published in Hart, for a range of 0 to 1 (TAN(45 degrees)) the form

 Fn = X * P(X * X) 

has a precision of only 9.43 decimal digits for N = 10 (Index 4994). And each additional increment of N appears to add about 0.8 additional digit of precision. After our experience developing our own series approximation for EXP with N = 6 we are not about to try to develop our own series approximation for ATN with N = 17 or so!

This means we had to look for an alternate method. Hart provides such a method involving reducing the range to 0 to about 0.098 (TAN(5.625 degrees)). Unfortunately the method is NOT simple, at least not for us. And to make things worse there appears to be a discrepancy between what Hart does and what Hart says it does! We will explain this later.

APPLICABILITY:

There is a corresponding arc (or angle) for any possible argument. Therefore no error testing need be performed.

 IDENTITIES (from Hart et al):

 eqn 6.5.3: ARCTAN(X) = ARCTAN(X) + kPI

 eqn 6.5.21 ARCTAN(-X) = - ARCTAN(X) 

Page 13, Column 2

(the following formulae are said to be derived from the earlier formula 6.5.27).

 T = 1/y - (1/(y * y) + 1)/(1/y + X)

 ARCTAN(X) = ARCTAN(y) + ARCTAN(T) 

DISCUSSION:

The two formulae above are given in Hart, section 6.5.e and are used in conjunction with a method of partitioning the argument so that the calculation can be made over the argument range 0 to 0.098 instead of 0 to 1. The text of Hart states that the argument, ranging from 0 to infinity, should be partitioned by eight partition points and that the appropriate constants are printed in Hart for those eight partition points.

The fact appears to be that the argument, ranging from 0 to 1, should be partitioned by four partition points and that appropriate constants are printed in Hart for these four partition points.

RANGE REDUCTION STRATEGY: If the sign is negative we set a sign flag and set the sign bit positive (take the absolute value of the argument). The argument is now in the range 0 to positive infinity. If the argument is greater than one we set an 'invert' flag and calculate the reciprocal of the argument. The range of the argument is now 0 to 1; we have two flags to test at the conclusion of the series approximation.

And NOW, boys and girls, the fun starts. We will use four partition points to partition the range 0 to 1 into five partitions. The partition points are:

 X1 = TAN(PI/32),     appx 0.098
 X2 = TAN(3PI/32),      "  0.303
 X3 = TAN(5PI/32),      "  0.535
 X4 = TAN(7PI/32),      "  0.821 

For each of these four partition points, we need four stored constants. The first stored constant is the partition point itself, used to determine which partition the argument fits into. The second constant is the RECIPROCAL of y used in the formulae above (Hart uses lower case x with the subscript i instead of y). The four y values are:

 y1 = TAN(PI/16),   appx 0.199
 y2 = TAN(PI/8),      "  0.414
 y3 = TAN(3PI/16),    "  0.668
 y4 = TAN(PI/4) = 1 exactly 

The third stored constant is equal to the second constant squared, plus one. Note that this is equal to (1/(y*y)+1) in the first formula on this page. The fourth stored constant is equal to the arc tangent of y, so that the four constants are simply PI/16, PI/8, 3PI/16 and PI/4.

Page 14, Column 1

Although we have five partitions, if the argument falls between 0 and 0.098 (appx) no range reduction is necessary. This is similar to the exponent calculation, where only fifteen stored constants were needed for sixteen partitions.

In the table beginning on line 744, Xn is the partition point for the nth partition, An is 1/y, Bn is (1/(y*y)+1) and Cn is the ARCTAN(y).

LET US TALK THROUGH a typical calculation. Say we have an argument of -1.6. We set the sign flag and clear the most significant bit of S1, setting FPACC1 equal to 1.6. Next we test whether FPACC1 is greater than one. It is, so we set the invert flag and invert FPACC1 by dividing it into the number one. The result is 0.625. Now we have to determine which partition we are in.

Is FPACC1 less than X1? No. So we add #32 to our table pointer and check whether FPACC1 is less than X2. Nope. Not until we compare FPACC1 to X4 will we discover that we are less than the stored partition point. That means that the correct partition lies between X3 (0.535) and X4 (0.821). We will now use constants A3 and B3 to reduce FPACC1 to the range -0.098 to 0.098 via the formula at the top of the preceding column.

First we add FPACC1 (0.625) to A3 (1/0.668), result (1/y + X) or about 2.121. We divide this into B3 (1/(0.688*0.688)+1), result equal to the portion of the first formula on the preceding column to the right of the minus sign. FPACC1 is now about 1.527. Now we subtract #16 from our table pointer to point to A3 again and subtract FPACC1 from A3. This completes the calculation of T, which is about -0.0305.

Now we use the series approximation Hart Index 4903, N = 5, precision 16.52, range 0, TAN(PI/32) or 0 to about 0.098. BUT, folks, our argument is not in that range! Which is another mild gripe we have about Hart. You see, since the series approximation has the form X * P(X * X) AND ARCTAN(-X) * - ARCTAN(X), the range of the approximation is actually -TAN(PI/32) to TAN(PI/32). Anyhow, the series approximation gives us the right result, which is about -0.0304.

You will note that the result of the series approximation is almost the same as its argument (input). THAT is why the series approximation over this limited range of -0.098 to 0.098 is so efficient; it is easy to find approximations for functions whose output is nearly equal to their input. And the reason we went through that mumbo-jumbo range reduction was to gain access to the efficient approximation. Verstad?

Page 14, Column 2

Having calculated ARCTAN(T), we have to add ARCTAN(y) to obtain what we want, which is ARCTAN(X), right? WRONG! We test to see whether the original argument was in the range 0 to 0.098, in which case no range reduction occurred and we ALREADY HAVE ARCTAN(X) as the result. So we check the pointer to Cn. It is not zero, so we know that range reduction WAS performed. So we use the Cn pointer to find C3 and add 3PI/16 to -0.0304 to get 0.559, which is ARCTAN(0.625).

We are NOT done yet. Remember the sign flag and the invert flag? First we check the invert flag and it is set. So now we determine a new arc by subtracting FPACC1 from PI/2 (which is 90 degrees). The result is about 1.012. Next we check the sign flag and it is set too, so we set the sign of the result negative.

So the final result of our calculation is -1.012, which is the ARCTAN of -1.6. If that number doesn't look right to you, remember we are working in radians. Our result is about -57.99 degrees if you want to convert radians to degrees by multiplying by 180/PI.

See how simple it is to calculate the ARCTAN function?

Getting specific about the code: the ARCTAN subroutine starts on line 660. Instead of actual flags, we store the original sign and exponent in location SINSGN for later testing for the equivalent of those two flags. To test which segment we are in, we place #32 in D6 and the table address, minus #32, in D7.

Then we call a subroutine at line 671 which adds D6 to D7, places the result in pointer A0, and compares FPACC1 with Xn in the table. If the first call of the subroutine at line 694 results in an indication that FPACC1 is less than X1, a branch (in line 695) to X0 at line 716, bypassing the range reduction.

If we bypass the range reduction process, we have to know we did so. That's why the very first line of the ARCTAN function clears EXPADD, which is used as a pointer to the appropriate Cn. AFTER the series calculation, we check this pointer at line 722, and skip adding Cn if the pointer is zero. If the pointer is NOT zero, we move it to A0 and call subroutine FPADD to add FPACC1 to Cn.

(We seem to be going into overtime, so this subject will be concluded next issue. The reader is advised that the TAN, ARCTAN and EXP functions have been thoroughly tested but the SQR, LOG, SIN and COS functions have NOT yet been thoroughly tested. However, the algorithms used for them are essentially unchanged from our 9 digit Microsoft compatible package. No bugs are anticipated other than simple typos.)

Page 15, Column 1

RUMORS AND INNUENDO:

IS IT TRUE that Charlie Winterble, Al Charpentier and an unnamed third engineer who left Commodore a couple of months back have come to roost at Atari? Charlie, besides being Commodore's former chief engineer, was the designer of the very fine sound chip in Commodore's Model 64 and doubtless played a major part in the design of the almost as good (for game-playing purposes) graphic controller chip also found in the Model 64. Can we expect to find EVEN BETTER sound and graphic controller chips in the Atari 1200, said to be ready for public unveiling in Feb '83??

IS IT TRUE that Al Charpentier purchased a new Mercedes two weeks after leaving Commodore? Did he pay for it with cash?

IS IT TRUE that the unnamed third member of Atari's Commodore Alumni Association is in fact the principal architect of Commodore's famous but unannounced 650,000 microprocessor (the number of zeros is said to be correct, anonymous sources indicate).

IS IT TRUE that, as a result of the loss of this principal architect the 650,000 project has been dropped at Commodore? Is it true that Atari has inadvertently done Commodore an ENORMOUS favor because the final design specification document for the 650,000, which is rumored to have 74 pages, reveals that the 650,000 is in fact a baby iAPX 432 we kid you not? Is it further true that this document was released on one of the first three days of Oct '81, a time when it was generally believed in the industry that the iAPX 432 would be a very high performance part?

IS IT TRUE that the final design document reportedly asserts on page 3, "(the 650,000 will have) ...capabilities somewhere between the 68000 and Intel's 432 micro-mainframe"? Is it further true that recent information which has come to light regarding the performance of the 432 indicates that that assertion would probably have been true had the project not been cancelled? Of course, the 8080 and 6502 ALSO have performance capabilities which lie between the 68000 and the iAPX 432...

According to an informed observer who declined to be named, "Commodore is on the verge of announcing an agreement with a manufacturer of 16 bit microprocessors", presumably to fill the void left by the (fortunately for Commodore) defunct 650,000 project. The manufacturer in question is neither Intel nor is it Motorola nor is it any of their second sources. We know who the manufacturer is but we promised not to tell...

Page 15, Column 2

IS IT TRUE that Commodore is experiencing severe financial difficulties, difficulties so severe that they recently had to sell an additional stock offering? Is it further true that the financial difficulties involve an inability to build factories fast enough to satisfy the public demand for their products? Is it true that a major competitor of Commodore located on the west coast has had NO DIFFICULTY WHATEVER in the past year building enough factories to keep up with public demand for their products? Why is Commodore unable to match the obvious management superiority of that west coast competitor?

IS IT TRUE that Tom Wolfe, the author of "The Right Stuff", a book about the beginnings of the astronaut program, is destined to write a book about a certain personal computer company which has in recent times shown an unwavering ability to select the worst possible decision at every available opportunity? Will that book be titled "The Wrong Stuff"??

IS IT TRUE that the absolutely totally confidential price list of a certain San Diego-based vendor of a personal computer operating system is printed on six different pieces of paper, one side only? Is it true that the quality of the paper stock rivals that used for the centerfold of certain girlie magazines? Is it true that the per copy royalty for small companies is MORE THAN NINE TIMES GREATER than the per copy royalty for large companies? Does this bear any relation to the fact that very few small companies have licensed that system for their 68000-based machines, even though the operating system is available for the 68000?

WE ARE ABLE TO REVEAL for the first time that Britain's Microcomputer Printout Magazine gossip columnist Inside Trader has moved to Newark, New Jersey. We have it on good authority that he prefers the living conditions in Armpit, er, Newark over those in Reading. However, he is reported to vigorously deny that the reception of several death threats from his fellow workers had anything to do with his decision to emigrate. We have faithfully promised the editor of Microcomputer Printout, Richard Paitson, not to reveal the source of this information...

IS IT TRUE that our Christmas card from the Apple Computer Co. is seriously overdue?

In a matter which is totally unrelated to any other item in this newsletter, IS IT TRUE that Zilog, which has been devoid of an ongoing domestic second source for its line of 16 bit microprocessors for exactly 13 months is about to sign an agreement which will fix that problem?

THIS MONTH'S AWARD:

IT IS TRUE that subscriber Leroy L. has been assigned this month's D-TACK D-Merit Award for suggesting that portions of this newsletter are more suitable for the National Enquirer than for a technical publication!

Code Listing

                          1          OPT     P=68000,BRS,FRS
                          2 ; NOTE: SEE BUG FIXES IN DG#17P22.
                          3 
                          4 ; MOTOROLA 68000 TRANSCENDENTAL PACKAGE
                          5 ;
                          6 ; WORKS WITH THE DOUBLE PRECISION FLOATING POINT
                          7 ; MATH PACKAGE USING A 48 BIT MANTISSA.
                          8 ;
                          9 ; COPYRIGHT 1982 DIGITAL ACOUSTICS INC.
                         10 ;
002600                   11          ORG     $2600          ;TEMP FOR DEVEL
                         12 ;
                         13 ; FOLLOWING ARE I/O ASSIGNMENTS:
                         14 ;
   # 00000FFA            15 STATUS   EQU     $0FFA
   # 00000FF8            16 DATIN    EQU     $0FF8
   # 00000FFA            17 DATOUT   EQU     $0FFA
                         18 ;
                         19 ; FOLLOWING ARE MEMORY ASSIGNMENTS
                         20 ; USED BY THE BOOTSTRAP ROM (MONITOR):
                         21 ;
   # 00000122            22 IDLE     EQU     $0122
   # 0000109C            23 ADR      EQU     $109C
   # 000010A0            24 N        EQU     $10A0
   # 000010A2            25 T        EQU     $10A2
                         26 ;
                         27 ; FOLLOWING ARE MEMORY ASSIGNMENTS FOR THIS CODE
                         28 ;
   # 000018F4            29 R        EQU     $18F4
   # 00001902            30 S1       EQU     R+14
   # 00001904            31 M1       EQU     S1+2
   # 0000190A            32 S2       EQU     S1+8
   # 0000190C            33 M2       EQU     S2+2
   # 00001912            34 FPT      EQU     S2+8
   # 0000191A            35 FPU      EQU     FPT+8
   # 00001922            36 LOGX     EQU     FPU+8
   # 00001922            37 SINSGN   EQU     LOGX
   # 00001924            38 SERCNT   EQU     LOGX+2
   # 00001926            39 EXPADD   EQU     LOGX+4         ;EXP ADDER
                         40 ;
   # 000023A8            41 FPADD    EQU     $23A8
   # 000023B0            42 FPADD1   EQU     $23B0
   # 000023A2            43 FPSUB    EQU     $23A2
   # 0000239A            44 FPSUB1   EQU     $239A
   # 00002220            45 FPMUL    EQU     $2220
   # 00002228            46 FPMUL1   EQU     $2228
   # 000022FA            47 FPDIV    EQU     $22FA
   # 00002302            48 FPDIV1   EQU     $2302
   # 000021DA            49 ERROR    EQU     $21DA
   # 000021D8            50 OVFL     EQU     $21D8
   # 000022F0            51 RZER     EQU     $22F0
   # 00002514            52 NORM     EQU     $2514
   # 00002570            53 SUBX     EQU     $2570
                         54 ;
002600  7E 03            55 ERR3     MOVEQ   #3,D7
002602  66 02            56          BNE     ERR4A
002604  7E 04            57 ERR4     MOVEQ   #4,D7
002606  4EF8 21DA        58 ERR4A    JMP     ERROR
                         59 ;
                         60 
                         61 ; COPYRIGHT 1982 DIGITAL ACOUSTICS, INC
                         62 ;
                         63 ; CALC LOG2 THEN MULT BY LOG10(2) RESULT LOG(10)
                         64 ;
00260A  61 0C            65 LOG10    BSR     LOG2           ;CALC LOG BASE 2
00260C  5048             66          ADDQ.W  #8,A0          ;PTR TO LOG10(2)
00260E  4EF8 2220        67          JMP     FPMUL          ;ACC = ACC * LOG(2)
                         68 ;
                         69 ; CALC LOG2(X) THEN MULT BY LOGE(2) RESULT LOGE(X)
                         70 ;
002612  61 04            71 LOGE     BSR     LOG2           ;CALC LOG BASE 2
002614  4EF8 2220        72          JMP     FPMUL          ;ACC = ACC * LN(2)
                         73 ;
                         74 ; CALCULATE THE LOGARITHM TO THE BASE 2
                         75 ;
002618  3038 1902        76 LOG2     MOVE.W  S1,D0
00261C  6B E2            77          BMI     ERR3           ;NO LOG IF NEG
00261E  0240 1FFF        78          ANDI.W  #$1FFF,D0      ;MASK UPPER BITS
002622  67 E0            79          BEQ     ERR4           ;NO LOG IF ZERO
                         80 ;
                         81 ; THE OPERAND IS LEGAL;  PROCEED WITH LOG2 CALC
                         82 ;
002624  0440 1000        83          SUBI.W  #$1000,D0      ;2'S COMP RESULT
002628  31C0 1922        84          MOVE.W  D0,LOGX        ;STORE INTGR PART
                         85 ;
                         86 ; SET THE OPERAND RANGE TO SQR(.5) =< X < SQR(2)
                         87 ;
00262C  31FC 1000 1902   88          MOVE.W  #$1000,S1
002632  307C 26BC        89          MOVE.W  #SQR2+2,A0     ;PTR TO SQR(2)
002636  4EB8 2B50        90          JSR     CMPM1          ;COMPARE MANTS
00263A  67 0A            91          BEQ     LOG2A          ;OK IF SAME
00263C  6A 08            92          BPL     LOG2A          ;OK IF FPACC1 >
                         93 ;
00263E  5278 1902        94          ADDQ.W  #1,S1          ;INCR EXPONENT
002642  5378 1922        95          SUBQ.W  #1,LOGX        ;DECR LOG EXP
                         96 ;
002646  4EB8 2756        97 LOG2A    JSR     FPZ            ;FPACC1 TO FP5
00264A  307C 26C2        98          MOVE.W  #LOGK,A0
00264E  4EB8 23A8        99          JSR     FPADD          ;CALC X-1
002652  4EB8 2764       100          JSR     M1U2           ;(X-1) TO FPU
002656  21F8 1912 1902  101          MOVE.L  FPT,S1         ;RECALL X
00265C  21F8 1916 1906  102          MOVE.L  FPT+4,S1+4
002662  4EB8 23A8       103          JSR     FPADD          ;CALC X+1
002666  21F8 191A 190A  104          MOVE.L  FPU,S2         ;(X-1) TO FPACC2
00266C  21F8 191E 190E  105          MOVE.L  FPU+4,S2+4
002672  4EB8 2302       106          JSR     FPDIV1         ;CALC (X-1)/(X+1)
                        107 ;
                        108 ; THE RANGE OF X IS NOW -0.172 TO +0.172. STORE
                        109 ; X IN FPU AND STORE Z= X*X IN FPT, FPACC1
                        110 ;
                        111 ; PERFORM SERIES EVALUATION, FORM IS Z*P(Z*Z)
                        112 ; WHERE Z = (X-1)/(X+1).
                        113 ;
002676  11FC 0006 1924  114          MOVE.B  #6,SERCNT      ;SET SERIES N = 7
00267C  4EB8 273C       115          JSR     SERSQU         ;DO SERIES EVAL
                        116 ;
                        117 
                        118 ; COPYRIGHT 1982 DIGITAL ACOUSTICS, INC.
                        119 ;
                        120 ; THE FRACTIONAL PART OF THE LOG2 IS COMPLETED
                        121 ;
002680  42B8 190A       122          CLR.L   S2             ;ZERO FPACC2
002684  42B8 190E       123          CLR.L   M2+2
002688  31F8 1922 190C  124          MOVE.W  LOGX,M2
00268E  67 1C           125          BEQ     LGEXIT         ;DONE IF LGEXP 0
002690  6B 1C           126          BMI     LGNEG          ;SKIP IF NEGATIVE
002692  3238 190C       127          MOVE.W  M2,D1          ;MANT2 TO D1
002696  303C 1010       128          MOVE.W  #$1010,D0      ;SET EXP = #16
00269A  5340            129 LOG2B    SUBQ.W  #1,D0          ;X2 = X2 - 1
00269C  E341            130          ASL.W   #1,D1          ;SHIFT MANT2 L
00269E  6A FA           131          BPL     LOG2B          ;REPT TILL D31= 1
0026A0  31C0 190A       132          MOVE.W  D0,S2          ;STORE X2 IN FPACC2
0026A4  31C1 190C       133          MOVE.W  D1,M2          ;STORE M2 IN FPACC2
0026A8  4EF8 23B0       134          JMP     FPADD1         ;ADD INTEGER; EXIT
                        135 ;
0026AC  4E75            136 LGEXIT   RTS                    ;LOG2 DONE
                        137 ;
                        138 ; THE INTEGER PORTION OF THE LOG IS NEGATIVE
                        139 ;
0026AE  303C 9010       140 LGNEG    MOVE.W  #$9010,D0      ;SET SIGN NEG
0026B2  4241            141          CLR.W   D1             ;(EXP IS 2'S COMP)
0026B4  9278 190C       142          SUB.W   M2,D1          ;ABS(EXPONENT)
0026B8  60 E0           143          BRA     LOG2B          ;ADD EXP TO LOG
                        144 ;
                        145 ;
                        146 ; CONSTANTS USED BY THE LOG ROUTINES
                        147 ;
0026BA  1001B504        148 SQR2     DC.L    $1001B504      ;SQR(2)
0026BE  F333F9DE        149          DC.L    $F333F9DE
0026C2  90018000        150 LOGK     DC.L    $90018000      ;MINUS 1
0026C6  00000000        151          DC.L    $00000000
0026CA  10018000        152 FPONE    DC.L    $10018000      ;ONE
0026CE  00000000        153          DC.L    $00000000
0026D2  0FFEFA61        154          DC.L    $0FFEFA61      ;P(6)
0026D6  18DC43A5        155          DC.L    $18DC43A5
0026DA  0FFF85C8        156          DC.L    $0FFF85C8      ;P(5)
0026DE  07A095A8        157          DC.L    $07A095A8
0026E2  0FFFA428        158          DC.L    $0FFFA428      ;P(4)
0026E6  9100003A        159          DC.L    $9100003A
0026EA  0FFFD30B        160          DC.L    $0FFFD30B      ;P(3)
0026EE  A7EE2159        161          DC.L    $A7EE2159
0026F2  100093BB        162          DC.L    $100093BB      ;P(2)
0026F6  628EF5FA        163          DC.L    $628EF5FA
0026FA  1000F638        164          DC.L    $1000F638      ;P(1)
0026FE  4EE1CAE4        165          DC.L    $4EE1CAE4
002702  1002B8AA        166          DC.L    $1002B8AA      ;P(0)
002706  3B395C18        167          DC.L    $3B395C18
00270A  1000B172        168          DC.L    $1000B172      ;LOGE(2)
00270E  17F7D1CF        169          DC.L    $17F7D1CF
002712  0FFF9A20        170          DC.L    $0FFF9A20      ;LOG10(2)
002716  9AA68151        171          DC.L    $9AA68151
                        172 ;
                        173 
                        174 ; COPYRIGHT 1982 DIGITAL ACOUSTICS, INC.
                        175 ;
                        176 ; PERFORM SERIES EVALUATION
                        177 ;
00271A  4EB8 2220       178 SERIES   JSR     FPMUL
00271E  60 10           179          BRA     SER2
002720  21F8 1912 190A  180 SER1     MOVE.L  FPT,S2
002726  21F8 1916 190E  181          MOVE.L  FPT+4,S2+4
00272C  4EB8 2228       182          JSR     FPMUL1         ;FPACC1 * FPT
002730  4EB8 23A8       183 SER2     JSR     FPADD          ;ADD NEXT P(I
002734  5338 1924       184          SUBQ.B  #1,SERCNT      ;DECR COUNT
002738  66 E6           185          BNE     SER1           ;LOOP UNTIL ZERO
00273A  4E75            186          RTS
                        187 ;
00273C  61 12           188 SERSQU   BSR     FPSQU          ;X SQUARED TO FPT
00273E  61 DA           189          BSR     SERIES         ;DO SERIES EVAL
                        190 ;
002740  21F8 191A 190A  191          MOVE.L  FPU,S2         ;FPU TO FPACC2
002746  21F8 191E 190E  192          MOVE.L  FPU+4,S2+4
00274C  4EF8 2228       193          JMP     FPMUL1         ;SQUARE IT; DONE
                        194 ;
                        195 ; LEAVE A COPY OF FPACC1 IN FPU, THEN
                        196 ; SQUARE IT AND LEAVE A COPY IN FPT
                        197 ;
002750  61 12           198 FPSQU    BSR     M1U2           ;FPACC1 TO FPACC2
002752  4EB8 2228       199          JSR     FPMUL1         ;SQUARE IT
002756  21F8 1902 1912  200 FPZ      MOVE.L  S1,FPT
00275C  21F8 1906 1916  201          MOVE.L  S1+4,FPT+4     ;LEAVE Z IN FPT
002762  4E75            202          RTS
                        203 ;
                        204 ; COPY FPACC1 TO FPU AND FPACC2
                        205 ;
002764  21F8 1902 191A  206 M1U2     MOVE.L  S1,FPU         ;FPACC1 TO FPU
00276A  21F8 1906 191E  207          MOVE.L  S1+4,FPU+4
                        208 ;
                        209 ; MOVE FPACC1 TO FPACC2
                        210 ;
002770  21F8 1902 190A  211 MOVE12   MOVE.L  S1,S2          ;FPACC1 TO FPACC2
002776  21F8 1906 190E  212          MOVE.L  S1+4,S2+4
00277C  4E75            213          RTS                    ;DONE
                        214 ;
                        215 
                        216 ; COPYRIGHT 1982 DIGITAL ACOUSTICS, INC.
                        217 ;
                        218 ; CALCULATE THE COSINE OF THE 68000 FPACC1
                        219 ;
00277E  08B8 0007 1902  220 SCOS     BCLR    #7,S1          ;SET FPACC1 POS
002784  307C 2D0C       221          MOVE.W  #COSK,A0       ;POINT A0 AT COSK
002788  4EB8 23A2       222          JSR     FPSUB          ;90 DEG - ACCUM
                        223 ;
                        224 ;
                        225 ; CALCULATE THE SINE OF THE 68000 FPACC#1
                        226 ;
00278C  11F8 1902 1922  227 SSIN     MOVE.B  S1,SINSGN      ;STORE THE SIGN
002792  08B8 0007 1902  228          BCLR    #7,S1          ;SET FPACC1 POS
002798  307C 2D14       229          MOVE.W  #SINK,A0       ;POINT A0 AT SINK
00279C  4EB8 2220       230          JSR     FPMUL          ;MULT BY 1/2#PI
0027A0  61 52           231          BSR     FRAC           ;RESULT UND 360 DEG
0027A2  5478 1902       232          ADDQ.W  #2,S1          ;MULT FPACC1 BY 4
0027A6  0C78 1002 1902  233          CMPI.W  #$1002,S1      ;FPACC1 < 2 ?
0027AC  65 16           234          BLO     UNDTWO         ;SKIP IF UNDER TWO
                        235 ;
                        236 ; TOGGLE THE SIGN AND SUBTRACT TWO
                        237 ;
0027AE  0878 0007 1922  238          BCHG    #7,SINSGN      ;TOGGLE SIGN
0027B4  21FC 90028000   239          MOVE.L  #$90028000,S2
        190A
0027BC  42B8 190E       240          CLR.L   S2+4           ;-2 TO FPACC2
0027C0  4EB8 23B0       241          JSR     FPADD1
                        242 ;
                        243 ; THE OPERAND IS NOW IN THE RANGE 0 TO 1.999999
                        244 ; IF LESS THAN ONE, PROCEED WITH CALCULATION,
                        245 ; ELSE SUBTRACT OPERAND FROM ONE AND PROCEED
                        246 ;
0027C4  0C78 1001 1902  247 UNDTWO   CMPI.W  #$1001,S1
0027CA  65 0E           248          BLO     UND1           ;SKIP IF < 1
                        249 ;
                        250 ; SET X = 90 DEGREES MINUS X
                        251 ;
0027CC  21F8 26CA 190A  252          MOVE.L  FPONE,S2
0027D2  42B8 190E       253          CLR.L   S2+4           ;ONE TO FPACC2
0027D6  4EB8 239A       254          JSR     FPSUB1         ;SUBTRACT
                        255 ;
                        256 ; THE RANGE OF X IS NOW 0 TO 0.99999999.
                        257 ; NOW PERFORM SERIES EVALUATION, N = 7
                        258 ;
0027DA  11FC 0007 1924  259 UND1     MOVE.B  #7,SERCNT      ;SET SERIES N = 7
0027E0  4EB8 273C       260          JSR     SERSQU         ;FORM X*P(X*X)
0027E4  11F8 1922 1902  261          MOVE.B  SINSGN,S1      ;RESTORE SIGN
0027EA  6A 06           262          BPL     SINX           ;EXIT IF SIGN POS
                        263 ;
0027EC  08F8 0007 1902  264          BSET    #7,S1          ;SET SIGN NEG
0027F2  4E75            265 SINX     RTS                    ;SINE CALC DONE
                        266 ;
                        267 
                        268 ; COPYRIGHT 1982 DIGITAL ACOUSTICS, INC.
                        269 ;
                        270 ; CALCULATE THE FRACTIONAL PART OF FPACC1
                        271 ;
0027F4  3438 1902       272 FRAC     MOVE.W  S1,D2          ;FETCH THE EXP
0027F8  3202            273          MOVE.W  D2,D1          ;SAVE SIGN
0027FA  0242 1FFF       274          ANDI.W  #$1FFF,D2      ;MASK THE SIGN BIT
0027FE  0C42 1000       275          CMPI.W  #$1000,D2      ;BR IF EQ OR LESS
002802  63 66           276          BLS     FRACX          ;DONE IF UNDER ONE
002804  0C42 1027       277          CMPI.W  #$1027,D2      ;NO FRACTION?
002808  6200 FAE6       278          BHI     RZER           ;RESULT IS ZERO
00280C  0442 1000       279          SUBI.W  #$1000,D2      ;CALC EXP- $1000
002810  0C42 0010       280          CMPI.W  #$10,D2        ;< 16 SHIFTS?
002814  63 26           281          BLS     UND16          ;SKIP IF LESS
                        282 ;
002816  0C02 0020       283          CMPI.B  #$20,D2        ; < 32 SHIFTS?
00281A  63 12           284          BLS     UND32          ;SKIP IF LESS
                        285 ;
                        286 ; WE HAVE 32 OR MORE SHIFTS TO PERFORM
                        287 ;
00281C  0402 0020       288          SUBI.B  #$20,D2
002820  4245            289          CLR.W   D5
002822  3838 1908       290          MOVE.W  M1+4,D4
002826  E56C            291          LSL.W   D2,D4
002828  4844            292          SWAP    D4
00282A  4244            293          CLR.W   D4
00282C  60 1E           294          BRA     FRO            ;NORMALIZE
                        295 ;
00282E  0402 0010       296 UND32    SUBI.B  #16,D2
002832  4245            297          CLR.W   D5
002834  2838 1906       298          MOVE.L  M1+2,D4
002838  E5AC            299          LSL.L   D2,D4
00283A  60 10           300          BRA     FRO            ;NORMALIZE
                        301 ;
00283C  2838 1904       302 UND16    MOVE.L  M1,D4
002840  3A38 1908       303          MOVE.W  M1+4,D5
002844  E34D            304 UND16A   LSL.W   #1,D5          ;-- SHIFT MANT
002846  E394            305          ROXL.L  #1,D4          ;   1 BIT LEFT --
002848  5342            306          SUBQ.W  #1,D2          ;DECR SHIFT COUNT
00284A  66 F8           307          BNE     UND16A         ;LOOP UNTIL DONE
                        308 ;
00284C  31FC 1000 1902  309 FRO      MOVE.W  #$1000,S1
002852  3001            310          MOVE.W  D1,D0          ;TEST SIGN
002854  6A 06           311          BPL     FSPOS          ;SKIP IF POS
002856  08F8 0007 1902  312          BSET    #7,S1          ;SET SIGN NEG
                        313 ;
                        314 ; NORMALIZE;  S1, X1 = MEM, M1 D4.L, D5.W
                        315 ;
00285C  2604            316 FSPOS    MOVE.L  D4,D3          ;NORMALIZED
00285E  6B 06           317          BMI     FR2            ;DONE OF NORMAL'D
                        318 ;
002860  4241            319          CLR.W   D1
002862  4EF8 2514       320          JMP     NORM           ;ELSE NORMALIZE
002866  4EF8 2570       321 FR2      JMP     SUBX           ;STORE RESULT, EXIT
00286A  4E75            322 FRACX    RTS
                        323 ;
                        324 
                        325 ; COPYRIGHT 1982 DIGITAL ACOUSTICS, INC.
                        326 ;
                        327 ; CALC THE SQUARE ROOT OF THE 68000 FPACC1
                        328 ;
00286C  3438 1902       329 SSQR     MOVE.W  S1,D2          ;CHK SIGN
002870  6B00 FD8E       330          BMI     ERR3           ;ERROR IF NEG
                        331 ;
                        332 ; THE OPERAND IS LEGAL; PROCEED WITH SQR CALC
                        333 ;
002874  0242 1FFF       334          ANDI.W  #$1FFF,D2      ;IS EXP ZERO?
002878  6700 FA76       335          BEQ     RZER           ;EXIT IF ZERO
00287C  2E38 1904       336          MOVE.L  M1,D7
002880  31FC 1000 1902  337          MOVE.W  #$1000,S1      ;1/2 =< X < 1
002886  3602            338          MOVE.W  D2,D3
002888  E24B            339          LSR.W   #1,D3          ;IS EXP EVEN?
00288A  64 06           340          BCC     EVNEXP         ;SKIP IF EVEN
00288C  5378 1902       341          SUBQ.W  #1,S1          ;DECR EXP
002890  E28F            342          LSR.L   #1,D7          ;MANT = MANT/2
                        343 ;
                        344 ; CALCULATE AND STORE THE EXP OF THE RESULT
                        345 ;
002892  363C 0800       346 EVNEXP   MOVE.W  #$0800,D3
002896  E24A            347          LSR.W   #1,D2
002898  D543            348          ADDX.W  D3,D2
00289A  31C2 1922       349          MOVE.W  D2,LOGX
                        350 ;
                        351 ; SET Y0 = $FFFF  (1ST GUESS DELIBERATELY HIGH)
                        352 ;
00289E  3E3C FFFF       353          MOVE.W  #$FFFF,D7
                        354 ;
                        355 ; PERFORM Y(N+1) = (Y(N) + X/Y(N))/2 4 TIMES
                        356 ;
0028A2  303C 0003       357          MOVE.W  #3,D0          ;SET FOR 4 LOOPS
0028A6  3A07            358          MOVE.W  D7,D5          ;Y0 = $FFFF
0028A8  2C07            359 SQL1     MOVE.L  D7,D6          ;MOVE X TO D6
0028AA  8CC5            360          DIVU    D5,D6          ;D6 = X/Y
0028AC  DA46            361          ADD.W   D6,D5          ;D5 = Y + X/Y
0028AE  E255            362          ROXR.W  #1,D5          ;DIV BY 2
0028B0  51C8 FFF6       363          DBF     D0,SQL1        ;LOOP 4 TIMES
                        364 ;
                        365 ; MOVE X TO TEMP FP REG U AND TO FPACC2
                        366 ;
0028B4  4EB8 2764       367          JSR     M1U2
                        368 ;
                        369 ; FLOAT THE 16 BIT APPROXIMATION
                        370 ;
0028B8  42B8 1906       371          CLR.L   M1+2
0028BC  31FC 1000 1902  372          MOVE.W  #$1000,S1
0028C2  31C5 1904       373          MOVE.W  D5,M1
0028C6  61 0A           374          BSR     SQITER         ;ONE ITERATION
0028C8  61 08           375          BSR     SQITER         ;ANOTHER ITER'TN
                        376 ;
                        377 ; RESTORE THE EXPONENT OF THE RESULT
                        378 ;
0028CA  31F8 1922 1902  379          MOVE.W  LOGX,S1        ;(SIGN IS POS)
0028D0  4E75            380          RTS
                        381 ;
                        382 
                        383 ; COPYRIGHT 1982 DIGITAL ACOUSTICS, INC.
                        384 ;
                        385 ; PERFORM ONE ITERATION OF Y1 = (Y0 + X/Y0)/2
                        386 ; FIRST MOVE Y0 TO TEMP FP REGISTER T
                        387 ;
0028D2  21F8 1902 1912  388 SQITER   MOVE.L  S1,FPT         ;Y0 TO FPT
0028D8  21F8 1906 1916  389          MOVE.L  S1+4,FPT+4
0028DE  21F8 191A 190A  390          MOVE.L  FPU,S2         ;X TO FPACC2
0028E4  21F8 191E 190E  391          MOVE.L  FPU+4,S2+4
0028EA  4EB8 2302       392          JSR     FPDIV1         ;CALC X/Y0
0028EE  307C 1912       393          MOVE.W  #FPT,A0        ;POINT AT Y0
0028F2  4EB8 23A8       394          JSR     FPADD          ;ADD Y0 TO X/Y0
0028F6  5378 1902       395          SUBQ.W  #1,S1          ;DIVIDE BY 2
0028FA  4E75            396          RTS                    ;ITERATION DONE
                        397 ;
                        398 ;
                        399 ; CALCULATE THE TANGENT FUNCTION IN RADIANS
                        400 ; FIRST REDUCE THE RANGE TO -180 DEG < X < 180 DEG
                        401 ;
0028FC  307C 29B6       402 STAN     MOVE.W  #TANK,A0       ;PTR TO 1/PI
002900  4EB8 2220       403          JSR     FPMUL          ;(#1 = 180 DEG)
002904  4EB8 27F4       404          JSR     FRAC           ;RESULT < 180 DEG
002908  307C 0000       405          MOVE.W  #0,A0          ;CLEAR FLAGS
00290C  31C8 1922       406          MOVE.W  A0,SINSGN      ;CLR SIGN FLAG
                        407 ;
                        408 ; REDUCE THE RANGE TO 0 =< X < 180 DEG
                        409 ;
002910  3238 1902       410          MOVE.W  S1,D1          ;S1, X1 TO D1
002914  6A 0C           411          BPL     TANPOS         ;SKIP IF POSITIVE
002916  08F8 0007 1922  412          BSET    #7,SINSGN      ;SET SIGN FLAG
00291C  08B8 0007 1902  413          BCLR    #7,S1          ;SET ARG POSITIVE
                        414 ;
                        415 ; REDUCE THE RANGE TO 0 =< X < 90 DEG
                        416 ;
002922  0C78 1000 1902  417 TANPOS   CMPI.W  #$1000,S1      ;FPACC < 1/2 ?
002928  65 14           418          BLO     TUH            ;SKIP IF < 1/2
00292A  0878 0007 1922  419          BCHG    #7,SINSGN      ;FLIP SIGN FLAG
002930  21F8 26CA 190A  420          MOVE.L  FPONE,S2       ;ONE TO FPACC2
002936  42B8 190E       421          CLR.L   S2+4
00293A  4EB8 239A       422          JSR     FPSUB1         ;180 DEG - X
                        423 ;
                        424 ; IF THE ARGUMENT IS 45 DEGREES OR MORE, SET
                        425 ; THE INVERT FLAG AND LET X = 90 DEG - X
                        426 ;
00293E  0C78 0FFF 1902  427 TUH      CMPI.W  #$0FFF,S1      ;FPACC < 1/4 ?
002944  65 12           428          BLO     TUQ            ;SKIP IF < 1/4
002946  5448            429          ADDQ.W  #2,A0          ;B1 IS INVERT FLAG
002948  21FC 10008000   430          MOVE.L  #$10008000,S2  ;1/2 TO FPACC2
        190A
002950  42B8 190E       431          CLR.L   S2+4
002954  4EB8 239A       432          JSR     FPSUB1         ;90 DEG - X
                        433 ;
                        434 ; ARGUMENT IS NOW LESS THAN 45 DEGREES; REDUCE
                        435 ; THE RANGE TO 22.5 DEGREES AND SET THE REDUCTION
                        436 ; (RED.) FLAG IF 22.5 DEG <= ARGUMENT.
                        437 ;
002958  0C78 0FFE 1902  438 TUQ      CMPI.W  #$0FFE,S1      ;FPACC < 1/8 ?
00295E  65 06           439          BLO     TUE            ;SKIP IF < 1/8
002960  5248            440          ADDQ.W  #1,A0          ;B0 IS RED. FLAG
002962  5378 1902       441          SUBQ.W  #1,S1          ;DIVIDE FPACC BY 2
                        442 ;
                        443 
                        444 ; COPYRIGHT 1982 DIGITAL ACOUSTICS, INC.
                        445 ;
                        446 ; THE ARGUMENT IS NOW LESS THAN 22.5 DEGREES;
                        447 ; PERFORM SERIES EVALUATION HART 4187 FORM X*P(X*X)
                        448 ;
002966  5678 1902       449 TUE      ADDQ.W  #3,S1          ;RANGE 0 TO 1
00296A  31C8 1926       450          MOVE.W  A0,EXPADD      ;RESTORE FLAGS
00296E  307C 29BE       451          MOVE.W  #TANK+8,A0     ;PTR TO SERIES K'S
002972  11FC 0008 1924  452          MOVE.B  #8,SERCNT      ;SET SERIES N = 8
002978  4EB8 273C       453          JSR     SERSQU         ;DO SERIES EVAL
                        454 ;
                        455 ; ADJUST FOR RANGE REDUCTION IF NEEDED
                        456 ;
00297C  E2F8 1926       457          LSR     EXPADD         ;TEST RED. FLAG
002980  64 18           458          BCC     NOTRNG         ;SKIP OF NOT SET
002982  4EB8 2750       459          JSR     FPSQU          ;X TO FPU; SQUARE
002986  307C 26CA       460          MOVE.W  #FPONE,A0      ;PTR TO 1
00298A  4EB8 23A2       461          JSR     FPSUB          ;1 - X*X
00298E  307C 191A       462          MOVE.W  #FPU,A0        ;PTR TO X
002992  4EB8 22FA       463          JSR     FPDIV          ;X/(1 - X*X)
002996  5278 1902       464          ADDQ.W  #1,S1          ;2X/(1 - X*X)
                        465 ;
                        466 ; INVERT IF THE INVERT FLAG IS SET
                        467 ;
00299A  E2F8 1926       468 NOTRNG   LSR     EXPADD         ;TEST INV. FLAG
00299E  64 08           469          BCC     NOTINV         ;SKIP IF NOT SET
0029A0  307C 26CA       470          MOVE.W  #FPONE,A0      ;PTR TO 1
0029A4  4EB8 22FA       471          JSR     FPDIV          ;INVERT FPACC1
                        472 ;
                        473 ; CHANGE THE SIGN IF THE SIGN FLAG IS SET
                        474 ;
0029A8  3038 1922       475 NOTINV   MOVE.W  SINSGN,D0      ;TEST SIGN FLAG
0029AC  6A 06           476          BPL     NOTNEG         ;SKIP IF NOT SET
0029AE  08F8 0007 1902  477          BSET    #7,S1          ;SET SIGN NEGATIVE
0029B4  4E75            478 NOTNEG   RTS                    ;TANGENT CALC DONE
                        479 ;
                        480 ; CONSTANTS USED BY THE TANGENT ROUTINE
                        481 ;
0029B6  0FFFA2F9        482 TANK     DC.L    $0FFFA2F9      ;1/PI
0029BA  836E4E44        483          DC.L    $836E4E44
0029BE  0FDFD967        484          DC.L    $0FDFD967      ;P8
0029C2  E1E426B5        485          DC.L    $E1E426B5
0029C6  0FE39C3D        486          DC.L    $0FE39C3D      ;P7
0029CA  CBC63642        487          DC.L    $CBC63642
0029CE  0FE7A369        488          DC.L    $0FE7A369      ;P6
0029D2  61F9A940        489          DC.L    $61F9A940
0029D6  0FEBA2F5        490          DC.L    $0FEBA2F5      ;P5
0029DA  68557947        491          DC.L    $68557947
0029DE  0FEFA2FA        492          DC.L    $0FEFA2FA      ;P4
0029E2  50DA798D        493          DC.L    $50DA798D
0029E6  0FF3A2FF        494          DC.L    $0FF3A2FF      ;P3
0029EA  FC90F626        495          DC.L    $FC90F626
0029EE  0FF7A335        496          DC.L    $0FF7A335      ;P2
0029F2  E33C201E        497          DC.L    $E33C201E
0029F6  0FFBA55D        498          DC.L    $0FFBA55D      ;P1
0029FA  E7312DAE        499          DC.L    $E7312DAE
0029FE  0FFFC90F        500          DC.L    $0FFFC90F      ;P0
002A02  DAA22169        501          DC.L    $DAA22169
                        502 ;
                        503 
                        504 ; COPYRIGHT 1982 DIGITAL ACOUSTICS, INC.
                        505 ;
002A06  21F8 26CA 1902  506 XRONE    MOVE.L  FPONE,S1       ;RESULT IS ONE
002A0C  42B8 1906       507          CLR.L   S1+4
002A10  4E75            508 EXP2X    RTS                    ;RETURN
                        509 ;
002A12  1038 1922       510 EXOVFL   MOVE.B  SINSGN,D0      ;SIGN NEGATIVE?
002A16  6B00 F8D8       511          BMI     RZER           ;RESULT ZERO IF SO
002A1A  70 01           512          MOVEQ   #1,D0          ;#1 = OVFL
002A1C  4EF8 21DA       513          JMP     ERROR          ;REPORT OVERFLOW
                        514 ;
                        515 ; CALCULATE THE EXPONENT FUNCTION, BASE 10
                        516 ; FIRST DIVIDE BY LOG10(2) AND THEN CALC EXP2
                        517 ;
002A20  307C 2CC4       518 XP10     MOVE.W  #NVLOG2,A0     ;PTR TO 1/LOG10(2)
002A24  4EB8 2220       519          JSR     FPMUL
002A28  60 08           520          BRA     XP2            ;CALC EXP BASE 2
                        521 ;
                        522 ; CALCULATE THE EXPONENT FUNCTION, BASE E
                        523 ; FIRST DIVIDE BY LOG10(2) AND THEN CALC EXP2
                        524 ;
002A2A  307C 2CC4       525 XPE      MOVE.W  #NVLOG2,A0     ;POINT TO 1/LOGE(2)
002A2E  4EB8 2220       526          JSR     FPMUL
                        527 ;
                        528 ; CALCULATE THE EXPONENT FUNCTION, BASE 2
                        529 ;
002A32  11F8 1902 1922  530 XP2      MOVE.B  S1,SINSGN      ;STORE THE SIGN
002A38  08B8 0007 1902  531          BCLR    #7,S1          ;SET SIGN POSITIVE
002A3E  42B8 1926       532          CLR.L   EXPADD         ;CLR EXP ADDER
002A42  3038 1902       533          MOVE.W  S1,D0          ;EXP TO D0
002A46  0240 1FFF       534          ANDI.W  #$1FFF,D0      ;MASK SIGN BIT
002A4A  67 BA           535          BEQ     XRONE          ;RESULT ONE IF ZERO
002A4C  0C40 0FFD       536          CMPI.W  #$0FFD,D0      ;LESS THAN 1/16?
002A50  65 24           537          BCS     EXP2A          ;SKIP OF UNDER 1/16
                        538 ;
002A52  323C 100D       539          MOVE.W  #$100D,D1      ;-- TEST FOR ARG
002A56  9240            540          SUB.W   D0,D1          ;  OUT OF RANGE --
002A58  6B B8           541          BMI     EXOVFL         ;OVFL IF X1>$100D
002A5A  67 B6           542          BEQ     EXOVFL         ;OVFL IF X1=$100D
                        543 ;
                        544 ; STORE THE INTEGER OF 16*FPACC1 IN EXPADD
                        545 ;
002A5C  2438 1904       546          MOVE.L  M1,D2
002A60  0641 000F       547          ADDI.W  #15,D1         ;CORRECT THE COUNT
002A64  E2AA            548          LSR.L   D1,D2          ;SHIFT COUNT IN D1
002A66  21C2 1926       549          MOVE.L  D2,EXPADD      ;STORE EXP ADDER
                        550 ;
002A6A  5878 1902       551          ADDQ.W  #4,S1          ;MULT FPACC1 * 16
002A6E  4EB8 27F4       552          JSR     FRAC           ;FRACTIONAL PART
002A72  5978 1902       553          SUBQ.W  #4,S1          ;DIV FPACC1 BY 16
                        554 ;
                        555 ; FPACC RANGE IS NOW 0 TO ALMOST 1/16
                        556 ; PERFORM SERIES EVALUATION FORM P(X)
                        557 ;
002A76  307C 2CD4       558 EXP2A    MOVE.W  #EXPK2,A0      ;PTR TO P(X)
002A7A  11FC 0006 1924  559          MOVE.B  #6,SERCNT      ;SET N = 6
002A80  4EB8 2756       560          JSR     FPZ            ;X TO FPT
002A84  4EB8 271A       561          JSR     SERIES         ;SERIES EVAL
                        562 ;
                        563 
                        564 ; COPYRIGHT 1982 DIGITAL ACOUSTICS, INC.
                        565 ;
                        566 ; NOW ADD THE INTEGER VALUE OF X TO THE EXP
                        567 ;
002A88  2038 1926       568          MOVE.L  EXPADD,D0      ;FETCH ADDER
002A8C  E888            569          LSR.L   #4,D0          ;LEAST BIT VAL = 1
002A8E  D178 1902       570          ADD.W   D0,S1          ;ADD TO X1
002A92  3038 1928       571          MOVE.W  EXPADD+2,D0    ;LOW 4 BITS = K
002A96  0240 000F       572          ANDI.W  #$000F,D0      ;MASK ALL BUT 4
002A9A  67 0C           573          BEQ     NOEXPK         ;SKIP IF ZERO
                        574 ;
                        575 ; MULTIPLY FPACC1 BY ONE OF FIFTEEN CONSTANTS
                        576 ;
002A9C  E748            577          LSL.W   #3,D0          ;MULTIPLY BY 8
002A9E  0640 2AB6       578          ADDI.W  #EXPK-8,D0     ;ADDR OF CONSTANT
002AA2  3040            579          MOVE.W  D0,A0          ;SET PTR A0
002AA4  4EB8 2220       580          JSR     FPMUL          ;MULTIPLY BY K(N)
                        581 ;
                        582 ; INVERT FPACC1 IF THE SIGN IS NEGATIVE
                        583 ;
002AA8  1038 1922       584 NOEXPK   MOVE.B  SINSGN,D0      ;TEST SIGN OF ARG
002AAC  6A00 FF62       585          BPL     EXP2X          ;DONE OF POS
002AB0  21F8 26CA 190A  586 INV      MOVE.L  FPONE,S2       ;#1 TO FPACC2
002AB6  42B8 190E       587          CLR.L   S2+4
002ABA  4EF8 2302       588          JMP     FPDIV1         ;EXIT VIA DIVIDE
                        589 ;
                        590 ; CONSTANTS USED TO CORRECT FOR RANGE REDUCTION
                        591 ;
002ABE  100185AA        592 EXPK     DC.L    $100185AA      ;EXP2(1/16)
002AC2  C367CC48        593          DC.L    $C367CC48      ;(7B14C1)
002AC6  10018B95        594          DC.L    $10018B95      ;EXP2(1/8)
002ACA  C1E3EA8C        595          DC.L    $C1E3EA8C
002ACE  100191C3        596          DC.L    $100191C3      ;EXP2(3/16)
002AD2  D373AB12        597          DC.L    $D373AB12      ;(C3360C)
002AD6  10019837        598          DC.L    $10019837      ;EXP2(1/4)
002ADA  F0518DB9        599          DC.L    $F0518DB9
002ADE  10019EF5        600          DC.L    $10019EF5      ;EXP2(5/16)
002AE2  326091A1        601          DC.L    $326091A1      ;(11AD98)
002AE6  1001A5FE        602          DC.L    $1001A5FE      ;EXP2(3/8)
002AEA  D6A9B151        603          DC.L    $D6A9B151
002AEE  1001AD58        604          DC.L    $1001AD58      ;EXP2(7/16)
002AF2  3EEA42A1        605          DC.L    $3EEA42A1      ;(4AC644)
002AF6  1001B504        606          DC.L    $1001B504      ;EXP2(1/2)
002AFA  F333F9DE        607          DC.L    $F333F9DE
002AFE  1001BD08        608          DC.L    $1001BD08      ;EXP2(9/16)
002B02  A39F580C        609          DC.L    $A39F580C      ;(36BEA3)
002B06  1001C567        610          DC.L    $1001C567      ;EXP2(5/8)
002B0A  2A115507        611          DC.L    $2A115507
002B0E  1001CE24        612          DC.L    $1001CE24      ;EXP2(11/16)
002B12  8C151F85        613          DC.L    $8C151F85      ;(80E3DC)
002B16  1001D744        614          DC.L    $1001D744      ;EXP2(3/4)
002B1A  FCCAD69D        615          DC.L    $FCCAD69D
002B1E  1001E0CC        616          DC.L    $1001E0CC      ;EXP2(13/16)
002B22  DEEC2A95        617          DC.L    $DEEC2A95      ;(E110FF)
002B26  1001EAC0        618          DC.L    $1001EAC0      ;EXP2(7/8)
002B2A  C6E7DD24        619          DC.L    $C6E7DD24
002B2E  1001F525        620          DC.L    $1001F525      ;EXP2(15/16)
002B32  7D152487        621          DC.L    $7D152487      ;(CC2C75)
                        622 ;
                        623 
                        624 ; COPYRIGHT 1992 DIGITAL ACOUSTICS, INC.
                        625 ;
                        626 ; COMPARE FPACC WITH FP# IN MEMORY
                        627 ;
                        628 ; IF FPACC IS GREATER, N=0  (BPL FPACC>MEM)
                        629 ; IF FPACC IS LESS,    N=1  (BMI FPACC<MEM)
                        630 ; IF FPACC IS SAME,    Z=1
                        631 ;
002B36  70 80           632 CPFP1M   MOVEQ   #$80,D0
002B38  72 80           633          MOVEQ   #$80,D1
002B3A  C010            634          AND.B   (A0),D0        ;MEMSIGN TO D0
002B3C  C238 1902       635          AND.B   S1,D1          ;FPACC SIGN TO D1
002B40  B001            636          CMP.B   D1,D0          ;COMPARE SIGNS
002B42  66 1A           637          BNE     NOTEQL         ;DONE IF NOT SAME
                        638 ;
002B44  1001            639          MOVE.B  D1,D0          ;BOTH SIGNS NEG?
002B46  6B 18           640          BMI     NEGCMP         ;BRANCH IF NEG
                        641 ;
                        642 ; COMPARE TWO POSITIVE NUMBERS
                        643 ;
002B48  3038 1902       644 CPFPOS   MOVE.W  S1,D0
002B4C  B058            645          CMP.W   (A0)+,D0       ;COMPARE EXP'S
002B4E  66 0E           646          BNE     NOTEQL         ;DONE IF NOT SAME
                        647 ;
                        648 ; COMPARE THE MANTISSA TO MEMORY
                        649 ;
002B50  2038 1904       650 CMPM1    MOVE.L  M1,D0
002B54  B098            651          CMP.L   (A0)+,D0       ;COMPARE 32 BITS
002B56  66 06           652          BNE     NOTEQL         ;DONE IF NOT SAME
                        653 ;
002B58  3038 1908       654          MOVE.W  M1+4,D0
002B5C  B090            655          CMP.L   (A0),D0        ;COMPARE LEAST 16
                        656 ;
002B5E  4E75            657 NOTEQL   RTS                    ;DONE
                        658 ;
002B60  3018            659 NEGCMP   MOVE.W  (A0)+,D0
002B62  B078 1902       660          CMP.W   S1,D0          ;COMPARE EXP'S
002B66  66 F6           661          BNE     NOTEQL         ;DONE IF NOT EQUAL
                        662 ;
002B68  2018            663          MOVE.L  (A0)+,D0
002B6A  B0B8 1904       664          CMP.L   M1,D0          ;COMPARE 32 BITS
002B6E  66 EE           665          BNE     NOTEQL         ;DONE IF NOT EQUAL
                        666 ;
002B70  3010            667          MOVE.W  (A0),D0
002B72  B078 1908       668          CMP.W   M1+4,D0
002B76  4E75            669          RTS                    ;DONE
                        670 ;
002B78  DE46            671 CPXN     ADD.W   D6,D7          ;ADD #32 TO D7
002B7A  3047            672          MOVE.W  D7,A0          ;SET PTR TO XN
002B7C  60 CA           673          BRA     CPFPOS         ;CMP FPACC, XN
                        674 ;
                        675 
                        676 ; COPYRIGHT 1982 DIGITAL ACOUSTICS, INC.
                        677 ;
                        678 ; CALCULATE THE ARC TANGENT FUNCTION IN RADIANS
                        679 ;
002B7E  4278 1926       680 SATN     CLR.W   EXPADD         ;CLR PTR
002B82  3038 1902       681          MOVE.W  S1,D0          ;S1,X1 TO D0
002B86  31C0 1922       682          MOVE.W  D0,SINSGN      ;STORE IN SINSGN
002B8A  08B8 0007 1902  683          BCLR    #7,S1          ;SET SIGN POS
002B90  0240 1FFF       684          ANDI.W  #$1FFF,D0      ;TEST IF EXP = 0
002B94  6700 F75A       685          BEQ     RZER           ;RESULT IS ZERO
002B98  0C40 1001       686          CMPI.W  #$1001,D0      ;ONE OR GREATER?
002B9C  65 04           687          BCS     UNDONE         ;SKIP IF NOT
002B9E  4EB8 2AB0       688          JSR     INV            ;CALC RECIPROCAL
                        689 ;
                        690 ; TEST WHETHER RANGE REDUCTION IS NECESSARY
                        691 ;
002BA2  7C 20           692 UNDONE   MOVEQ   #32,D6         ;D6 = #32
002BA4  3E3C 2C24       693          MOVE.W  #X1-32,D7
002BA8  61 CE           694          BSR     CPXN           ;COMPARE X1
002BAA  6B 2A           695          BMI     X0             ;NO REDUCTION
002BAC  61 CA           696          BSR     CPXN           ;COMPARE X2
002BAE  6B 0A           697          BMI     XN             ;REDUCE ON X1-X2
002BB0  61 C6           698          BSR     CPXN           ;COMPARE X3
002BB2  6B 06           699          BMI     XN             ;REDUCTE ON X2-X3
002BB4  61 C2           700          BSR     CPXN           ;REDUCT ON X4
002BB6  6B 02           701          BMI     XN             ;REDUCE ON X3-X4
002BB8  DE46            702          ADD.W   D6,D7          ;REDUCE ON X4-PI/4
                        703 ;
002BBA  5147            704 XN       SUBQ.W  #8,D7          ;POINT TO CN
002BBC  31C7 1926       705          MOVE.W  D7,EXPADD      ;STORE CN ADDR
002BC0  0447 0010       706          SUBI.W  #16,D7         ;POINT TO AN
002BC4  3047            707          MOVE.W  D7,A0
002BC6  4EB8 23A8       708          JSR     FPADD          ;X + AN
002BCA  4EB8 22FA       709          JSR     FPDIV          ;BN/(X+AN)
002BCE  90FC 0010       710          SUB.W   #16,A0         ;PTR TO AN
002BD2  4EB8 23A2       711          JSR     FPSUB          ;AN-BN/(X+AN)
                        712 ;
                        713 ; RANGE REDUCTION TO -X1 TO X1 ACCOMPLISHED
                        714 ; PERFORM SERIES EVALUATION;  FORM IS X*P(X*X)
                        715 ;
002BD6  11FC 0005 1924  716 X0       MOVE.B  #5,SERCNT      ;SET N = 5
002BDC  307C 2C14       717          MOVE.W  #ATNK,A0       ;PTR TO ATN CONSTS
002BE0  4EB8 273C       718          JSR     SERSQU         ;DO SERIES EVAL
                        719 ;
                        720 ; ADD CN IF RANGE REDUCTION WAS DONE
                        721 ;
002BE4  3E38 1926       722          MOVE.W  EXPADD,D7      ;FETCH CN PTR
002BE8  67 06           723          BEQ     NOPTR          ;SKIP IF ZERO
002BEA  3047            724          MOVE.W  D7,A0          ;PTR TO CN
002BEC  4EB8 23A8       725          JSR     FPADD          ;ADD CN
                        726 ;
                        727 ; CORRECT FOR PREVIOUS INVERSION IF NEEDED
                        728 ;
002BF0  3038 1922       729 NOPTR    MOVE.W  SINSGN,D0      ;RECALL S1, X1
002BF4  0240 1FFF       730          ANDI.W  #$1FFF,D0      ;MASK SIGN BIT
002BF8  0C40 1001       731          CMPI.W  #$1001,D0      ;ONE OR GREATER?
002BFC  65 08           732          BCS     NOINV          ;SKIP IF NOT
002BFE  307C 2D0C       733          MOVE.W  #COSK,A0       ;PTR TO PI/2
002C02  4EB8 23A2       734          JSR     FPSUB          ;90 DEG - FPACC1
                        735 ;
                        736 
                        737 ; COPYRIGHT 1982 DIGITAL ACOUSTICS, INC.
                        738 ;
                        739 ; CHANGE SIGN IF ARGUMENT WAS NEGATIVE
                        740 ;
002C06  3038 1922       741 NOINV    MOVE.W  SINSGN,D0      ;RECALL S1
002C0A  6A 06           742          BPL     ATNX           ;DONE IF POS
002C0C  0878 0007 1902  743          BCHG    #7,S1          ;ELSE CHANGE SIGN
002C12  4E75            744 ATNX     RTS                    ;ARC TAN DONE
                        745 ;
                        746 ; CONSTANTS USED TO EVALUATE ARC TANGENT
                        747 ;
002C14  8FFDB5AB        748 ATNK    DC.L    $8FFDB5AB       ;P5
002C18  6364E40E        749         DC.L    $6364E40E
002C1C  0FFDE381        750         DC.L    $0FFDE381       ;P4
002C20  AEE4C3E4        751         DC.L    $AEE4C3E4
002C24  8FFE9249        752         DC.L    $8FFE9249       ;P3
002C28  1C8532D1        753         DC.L    $1C8532D1
002C2C  0FFECCCC        754         DC.L    $0FFECCCC       ;P2
002C30  CCC81F2E        755         DC.L    $CCC81F2E
002C34  8FFFAAAA        756         DC.L    $8FFFAAAA       ;P1
002C38  AAAAAA2B        757         DC.L    $AAAAAA2B
002C3C  10018000        758         DC.L    $10018000       ;P0
002C40  00000000        759         DC.L    $00000000
                        760 ;
                        761 ; CONSTANTS USED TO ADJUST RANGE OF ATN CALC
                        762 ;
002C44  0FFDC9B5        763 X1      DC.L    $0FFDC9B5       ;X1
002C48  DC62D96D        764         DC.L    $DC62D96D
002C4C  1003A0DF        765         DC.L    $1003A0DF       ;A1
002C50  F712123C        766         DC.L    $F712123C
002C54  1005D231        767         DC.L    $1005D231       ;B1
002C58  718DED74        768         DC.L    $718DED74
002C5C  0FFEC90F        769         DC.L    $0FFEC90F       ;C1 = PI/16
002C60  DAA22169        770         DC.L    $DAA22169
002C64  0FFF9B50        771 X2      DC.L    $0FFF9B50       ;X2
002C68  41AAE31F        772         DC.L    $41AAE31F
002C6C  10029A82        773         DC.L    $10029A82       ;A2
002C70  7999FCEF        774         DC.L    $7999FCEF
002C74  1003DA82        775         DC.L    $1003DA82       ;B2
002C78  7999FCEF        776         DC.L    $7999FCEF
002C7C  0FFFC90F        777         DC.L    $0FFFC90F       ;C2 = 2PI/16
002C80  DAA22169        778         DC.L    $DAA22169
002C84  100088D5        779 X3      DC.L    $100088D5       ;X3
002C88  B8C841A7        780         DC.L    $B8C841A7
002C8C  1001BF90        781         DC.L    $1001BF90       ;A3
002C90  C712D3A3        782         DC.L    $C712D3A3
002C94  1002CF59        783         DC.L    $1002CF59       ;B3
002C98  5AEEA7CA        784         DC.L    $5AEEA7CA
002C9C  100096CB        785         DC.L    $100096CB       ;C3 = 3PI/16
002CA0  E3F9990F        786         DC.L    $E3F9990F
002CA4  1000D218        787 X4      DC.L    $1000D218       ;X4
002CA8  01572142        788         DC.L    $01572142
002CAC  10018000        789         DC.L    $10018000       ;A4
002CB0  00000000        790         DC.L    $00000000
002CB4  10028000        791         DC.L    $10028000       ;B4
002CB8  00000000        792         DC.L    $00000000
002CBC  1000C90F        793         DC.L    $1000C90F       ;C4 = 4PI/16
002CC0  DAA22169        794         DC.L    $DAA22169
                        795 ;
                        796 
                        797 ; COPYRIGHT 1982 DIGITAL ACOUSTICS, INC.
                        798 ;
002CC4  1002D49A        799 NVLOG2  DC.L    $1002D49A       ;1/LOG10(2)
002CC8  784BCD1C        800         DC.L    $784BCD1C
002CCC  1001B8AA        801 INVLN2  DC.L    $1001B8AA       ;1/LOGE(2)
002CD0  3B295C18        802         DC.L    $3B295C18
                        803 ;
                        804 ; P(X); N= 6
                        805 ;
002CD4  0FF58B70        806 EXPK2   DC.L    $0FF58B70       ;P6
002CD8  00000000        807         DC.L    $00000000
002CDC  0FF7ABBF        808         DC.L    $0FF7ABBF       ;P5
002CE0  80000000        809         DC.L    $80000000
002CE4  0FFA9D9C        810         DC.L    $0FFA9D9C       ;P4
002CE8  CC200000        811         DC.L    $CC200000
002CEC  0FFCE358        812         DC.L    $0FFCE358       ;P3
002CF0  36210000        813         DC.L    $36210000
002CF4  0FFEF5FD        814         DC.L    $0FFEF5FD       ;P2
002CF8  F00C0800        815         DC.L    $F00C0800
002CFC  1000B172        816         DC.L    $1000B172       ;P1
002D00  17F7CD00        817         DC.L    $17F7CD00
002D04  10018000        818         DC.L    $10018000       ;P0
002D08  00000000        819         DC.L    $00000000
                        820 ;
                        821 ; CONSTANTS USED BY THE COSINE AND SINE CALCS
                        822 ;
002D0C  1001C90F        823 COSK    DC.L    $1001C90F       ;#PI/2
002D10  DAA22169        824         DC.L    $DAA22169
002D14  0FFEA2F9        825 SINK    DC.L    $0FFEA2F9       ;1/(2#PI)
002D18  836E4E44        826         DC.L    $836E4E44
                        827 ;
                        828 ; FORMULA 3344 HART,  FORM X*P(X*X)
                        829 ;
002D1C  8FE2B131        830 SINK1   DC.L    $8FE2B131       ;P7
002D20  3233A218        831         DC.L    $3233A218
002D24  0FE8F44E        832         DC.L    $0FE8F44E       ;P6
002D28  7501852C        833         DC.L    $7501852C
002D2C  8FEEF183        834         DC.L    $8FEEF183       ;P5
002D30  11E19C26        835         DC.L    $11E19C26
002D34  0FF4A83C        836         DC.L    $0FF4A83C       ;P4
002D38  1924E79B        837         DC.L    $1924E79B
002D3C  8FF99969        838         DC.L    $8FF99969       ;P3
002D40  6670BE99        839         DC.L    $6670BE99
002D44  0FFDA335        840         DC.L    $0FFDA335       ;P2
002D48  E33BA883        841         DC.L    $E33BA883
002D4C  9000A55D        842         DC.L    $9000A55D       ;P1
002D50  E7312DEB        843         DC.L    $E7312DEB
002D54  1001C90F        844         DC.L    $1001C90F       ;P0
002D58  DAA22169        845         DC.L    $DAA22169
                        846 ;